문제 링크 (2025/5/28 기준) Platinum III

문제 읽기

6개의 버튼이 달려있는 독특한 계산기가 있습니다. 계산기에는 초기에 정수 $x=0$이 저장되어 있고, 6개의 버튼은 각각 다음과 같은 연산을 수행합니다.

• sin: $x$를 $\sin x$로 바꿉니다.
• cos: $x$를 $\cos x$로 바꿉니다.
• tan: $x$를 $\tan x$로 바꿉니다.
• asin: $x$를 $\arcsin x$로 바꿉니다.
• acos: $x$를 $\arccos x$로 바꿉니다.
• atan: $x$를 $\arctan x$로 바꿉니다.

두 정수 $a$, $b$ $(1 \le a, b \le 10)$이 주어졌을 때, $\frac{a}{b}$의 값을 $1000$번의 연산 이내로 구해봅시다. 단, 절대 오차가 $10^{-9}$ 이내여야 합니다.

관찰

1. 초기에 $0$이 저장되어 있는데, $\cos 0 = 1$이므로, cos연산 한 번으로 $1$을 만들 수 있습니다. $a = b$라면, cos연산 한 번으로 $\frac{a}{b}$의 값을 정확하게 구할 수 있습니다.

2. 두 양의 정수 $p$, $q$에 대하여, $\frac{p}{q}$를 $\frac{q}{p}$로, 즉, 현재 저장되어 있는 값을 역수로 바꿀 수 있을까요? 놀랍게도 가능합니다.

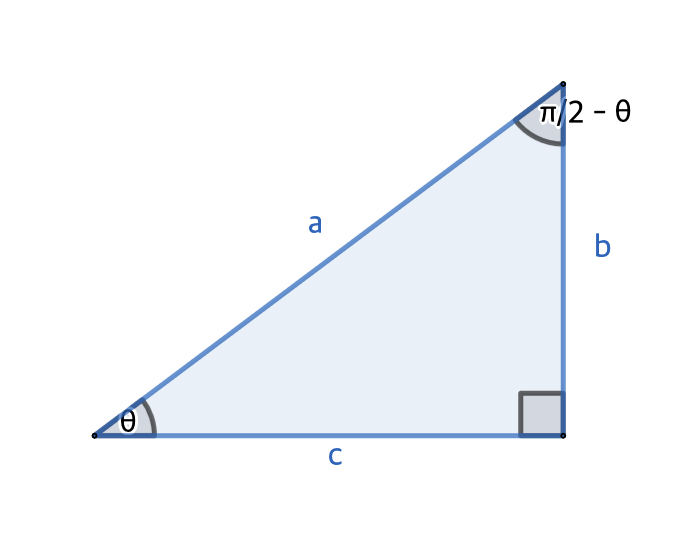
위 그림에서 $a^2 = b^2 + c^2$이고, $b$와 $c$를 가지고 $\frac{b}{c}$를 $\frac{c}{b}$로 바꿔봅시다. 우선, $\tan \theta = \frac{b}{c}$이므로, $\arctan \frac{b}{c} = \theta$를 통해 $\theta$를 얻을 수 있습니다. $\frac{c}{b} = \tan\left(\theta - \frac{\pi}{2} \right)$를 얻고 싶기 때문에, $\frac{\pi}{2} - \theta$의 값을 알고 싶습니다. $\cos \left(\frac{\pi}{2} - \theta\right) = \cos \left(\theta - \frac{\pi}{2} \right) = \sin \theta$이기 때문에, $\theta$를 $\frac{\pi}{2} - \theta$로 바꿀 수 있습니다. 이후, $\tan\left(\theta - \frac{\pi}{2} \right) = \frac{c}{b}$이므로, 연산 4번만으로 역수를 구하는 데 성공했습니다. 그림에서 보이는 대로 $0 < \theta < \frac{\pi}{2}$이므로, 계산 도중에 삼각함수의 정의역을 벗어나는 문제는 고려하지 않아도 됩니다.

즉, atan→sin→acos→tan 순으로 연산을 적용하면, 역수를 구할 수 있습니다.

3. (핵심) 문제에서 주어지는 $\frac{a}{b}$를 직각삼각형 한 각의 사인 값으로 생각해봅시다. 직각삼각형에서의 $\sin \theta$의 범위가 $0 < \sin \theta < 1$이므로, 만약 $a > b$라면 관찰 2. 를 이용해서 역수로 바꿔줍니다.

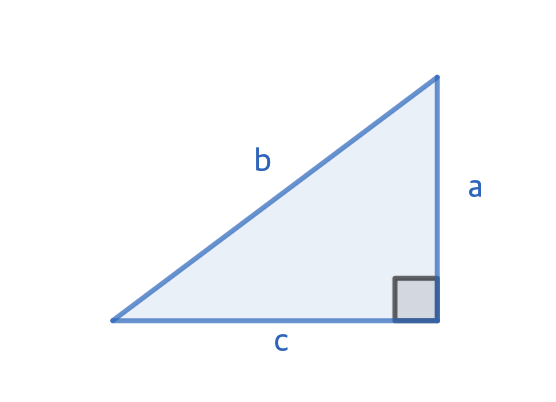
위 그림과 변 $a$, $b$, $c$의 위치가 문제 조건에 맞도록 달라졌음에 유의하세요. $a < b$가 성립하도록 하였고, 피타고라스 정리에 의해, 자명하게 $c < b$입니다. 따라서, $\frac{a}{c}$에 atan연산을 수행한 후 sin연산을 수행해서 $\frac{a}{b}$을 만들 수 있습니다. 그러면, $c = \sqrt{b^2 - a^2}$이고, $b := c$를 한 뒤, 위 과정을 재귀적으로 수행하다보면 결국 $\frac{1}{1}$이 됩니다. $1$이라는 값은 관찰 1. 을 이용해서 얻어낼 수 있습니다.

증명

$\gcd(a, b) \neq 1$이라면 최대공약수로 $a$와 $b$를 나눠서, $\frac{a}{b}$를 기약분수로 만들어 줍시다. $a$, $b$는 서로소입니다. 편의상, 루트가 나오지 않도록 모든 변의 길이를 제곱해서 사용합시다. $\gcd(a, b) = 1$이므로, $\gcd(a^2, b^2) = 1$임도 자명합니다. $c^2 = b^2 - a^2$인데, $c^2$와 $a^2$는 서로소입니다.

이유는 다음과 같습니다. $g = \gcd(a^2, c^2 = b^2 - a^2)$이라면, $g \vert a^2$이고, $g \vert (b^2 - a^2)$이므로, $g \vert (a^2 + b^2 - a^2 = b^2)$여야 합니다. $\gcd(a^2, b^2) = 1$이므로, 가능한 $g$의 값은 $1$로 유일합니다.

따라서, 새로 얻은 $a^2$와 $b^2$도 서로소임을 알 수 있고, $a^2 < b^2$이므로, 분자 또는 분모가 $0$이 되는 경우는 존재할 수 없습니다. 또한, 과정을 반복할수록 두 값은 단조감소하고, 둘 중 더 큰 값인 $b^2$가 $1$ 미만이 될 수 없으므로, $a = b = 1$인 상태로 유한 번의 반복 안에 종료되게 됩니다.$\square$

풀이

$\gcd(a, b)$로 $a$, $b$를 나눠서 기약분수 꼴로 나타내준 뒤, 관찰 3. 을 반복하여, $a^2$와 $b^2$가 각각 $1$이 될 때까지 각각의 스텝을 역순으로 기록하면 끝입니다. $a$와 $b$가 최대 $10$으로, 상당히 작습니다. 따라서, $1000$번의 연산으로 충분합니다.

코드

use std::{collections::VecDeque, fmt::Write, io::{stdin, Read}, mem::swap, str::SplitWhitespace};
 
fn main() {
    let mut buf = String::new();
    let mut out = String::new();
 
    stdin().read_to_string(&mut buf).unwrap();
    let mut scan = Scanner::new(buf.split_whitespace());
    
    let mut tc = 1;
    if tc != 1 { tc = scan.next::<usize>(); }
    for _ in 0..tc {
        solve(&mut scan, &mut out);
    }
    print!("{out}");
}

fn solve<'a>(scan: &mut Scanner<'a, SplitWhitespace<'a>>, out: &mut String) {
    let mut a: usize = scan.next();
    let mut b: usize = scan.next();
    let g = gcd(a, b);
    a = (a / g) * (a / g);
    b = (b / g) * (b / g);
    let mut ops = VecDeque::new();
    while a * b != 1 {
        if a > b {
            swap(&mut a, &mut b);
            ops.push_back("tan");
            ops.push_back("acos");
            ops.push_back("sin");
            ops.push_back("atan");
        }
        ops.push_back("sin");
        ops.push_back("atan");
        b -= a;
    }

    ops.push_back("cos");
    writeln!(out, "{}", ops.len()).ok();
    for i in (0..ops.len()).rev() {
        write!(out, "{} ", ops[i]).ok();
    }
}

fn gcd(a: usize, b: usize) -> usize {
    let mut n1 = a;
    let mut n2 = b;
    
    if n1 < n2 {
        swap(&mut n1, &mut n2);
    }
    while n1 % n2 != 0 {
        let r = n1 % n2;
        n1 = n2;
        n2 = r;
    }

    n2
}

struct Scanner<'a, I: Iterator<Item = &'a str>> {
    iter: I,
}
 
impl<'a, I: Iterator<Item = &'a str>> Scanner<'a, I> {
    fn new(from: I) -> Self {
        Self { iter: from }
    }
    fn next<T: std::str::FromStr>(&mut self) -> T {
        self.iter.next().unwrap().parse().ok().unwrap()
    }
}

처음에 연산을 거꾸로 기록하면서 스택을 쓰면 될 줄 알았는데, 그냥 벡터를 거꾸로 훑으면 그만이더라고요… 벡터를 사용해도 무방합니다.

후기

근 몇 주간 풀었던 문제 중에서 가장 재밌는 문제 같습니다. 조금 발상적이지만, 정말 주어진 연산의 성질을 관찰하다보면 아름답고 깔끔하게 풀리는데다, 증명까지 너무 재밌었습니다. 이런 비슷한 문제가 더 많았으면 좋겠습니다.